【入門】 微粒子の粒子径(粒径)測定
5.動的光散乱法の解析原理
光子相関法で求めた自己相関関数よりキュムラント法で平均粒子径d(流体力学的径)および多分散指数を、 ヒストグラム法で粒子径分布を求めます。
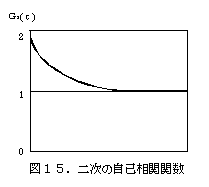
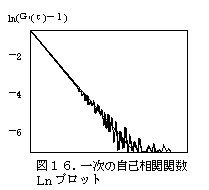
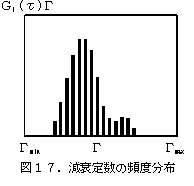
| ●自己相関関数 散乱強度の時間変化から直接求められる二次の自己相関関数 G2(τ)は次式で表されます。 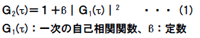 粒子が単分散の場合、G1(τ)は単一指数減衰曲線となり、 減衰定数Γを用いて次のように表されます。 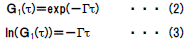 Γは並進拡散係数Dを用いて次のように表されます。 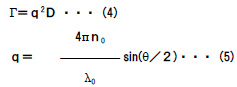 q:散乱ベクトル、 n0:溶媒の屈折率、 λ0:レーザー光の波長 ●アインシュタイン・ストークスの式 アインシュタイン・ストークスの式を用いて、拡散係数から 粒子径(粒径)【ストークス径】が求められます。 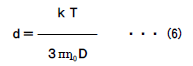 d:粒子径(流体力学的直径)、 k:ボルツマン定数、 T:絶対温度、η:溶媒の粘度 ●キュムラント法解析 キュムラント法では指数部をτで二次級数展開をおこなって 近似します。 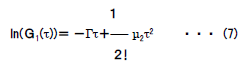 キュムラント平均粒子径は、 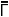 から得られます。 多分散指数は、μ2を から得られます。 多分散指数は、μ2を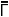 の二乗で規格化(μ2/ の二乗で規格化(μ2/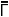 2)することで得られ、粒子径分布の多分散度を示します。 2)することで得られ、粒子径分布の多分散度を示します。●ヒストグラム法解析 ヒストグラム法では、有限個数のΓjで分布を代表させて、非線形最小自乗法などを用いて近似します。 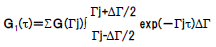 各減衰定数を(4)(6)式を用いて粒子径に換算します。これを 横軸とし、ここで得られた頻度を縦軸としてヒストグラム表示することで、粒子径分布(粒径分布)が得られます。 |
    |
【動的光散乱法の概要】
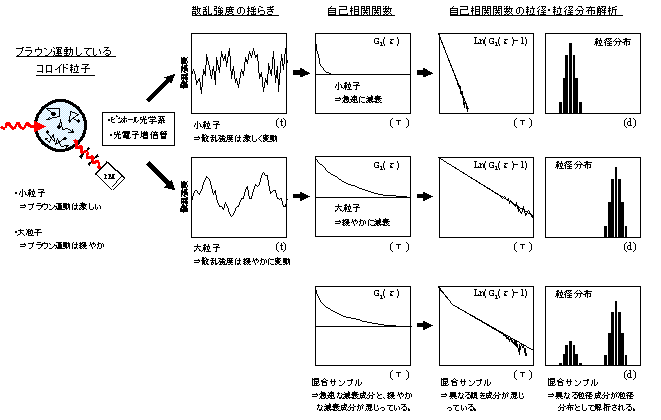


 Close
Close








