【入門】 微粒子の粒子径（粒径）測定

懸濁溶液や溶液中に分散した微粒子は、通常ブラウン運動をしており、その動きは大きな粒子では遅く、小さな粒子になるほど早くなります。この時、ブラウン運動をしている粒子にレーザー光を照射すると、粒子からの散乱光はそれぞれのブラウン運動の速度に対応した揺らぎが観測されます。

動的光散乱法では、図５に示すように溶液中に分散している粒子にレーザー光を照射し、その散乱光を光子検出器で観測します。この時、粒子からの散乱光はYoungの光干渉実験モデル（図６）の様に干渉し合います。さらに粒子はブラウン運動によりその位 置を絶えず移動しているため、散乱光の干渉による強度分布も絶えず揺らぐことになります。このため、ピンホールや光ファイバー系の光学系をもちいると、このブラウン運動の様子を散乱光強度の揺らぎとして観測することが出来ます。

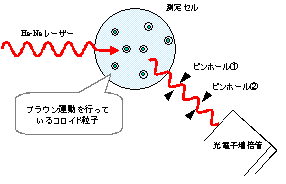
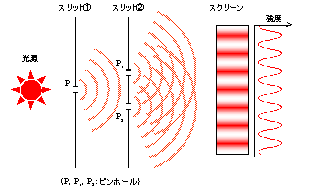
図５．動的光散乱法の測定概略図　　　　　　　　図６．Youngの光干渉実験モデル

観測された散乱光の時間的な揺らぎ変動は、図７，８の様に粒子径によって変動する様子が異なります。

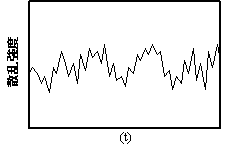
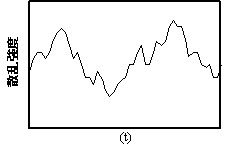
図７．小粒子の散乱光の揺らぎ　　　　図８.大粒子の散乱光のゆらぎ

この揺らぎを観測し、光子相関法により自己相関関数を求め、キュムラント法およびヒストグラム法解析を用いることで、ブラウン運動速度を示す拡散係数、さらに粒子径や粒子径分布が求められます。

自己相関関数は、任意の時間(t)における散乱強度I(t)を基準とし、(τ)時間後の散乱強度I(t+τ)についての相関を、次式のように表します。

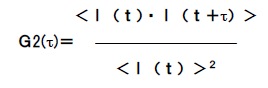
ここで、＜＞は平均を表します。この自己相関関数は時間(τ)のみに依存し、測定開始時間(t)には依存しなくなります。
自己相関関数では、τが小さい時には粒子はあまり移動していないため散乱光量の変化は小さく高い相関を示しますが、τが大きくなると粒子の位 置は不確定になるため散乱光量もランダムに変化し相関はほとんど見られなくなります。このため、得られた自己相関関数は指数関数的な減衰曲線になります。

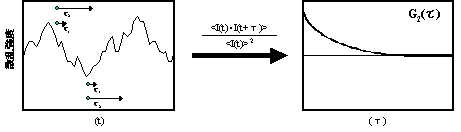
図９．散乱光強度と自己相関関数

粒子は右図のようにブラウン運動によりその位 置を変えています。自己相関関数では，ある基準時間の時の粒子の位置からτ1，τ2，τ3… の間での粒子の重なり合いの度合いを時間の関数として表しています。その結果、図１１に示すように、時間が経つにつれて重なり度合いは少なくなるため、自己相関関数Ｇ2(τ)は時間とともに減衰する関数となります。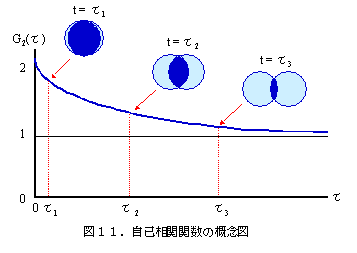

（第１２回散乱研究会「動的光散乱－基礎セミナー」 （東京大学　柴山充弘教授）の資料を参照しました。）

散乱強度の変動を光子相関法を用いて解析すると、小さな粒子の場合は相関時間の短い相関関数が、大きな粒子の場合は相関時間の長い相関関数が得られます。相関関数は、浮遊粒子の並進運動ブラウン運動に関する情報を含んでおり、計算式により粒子径や粒子径分布を求めることができます。

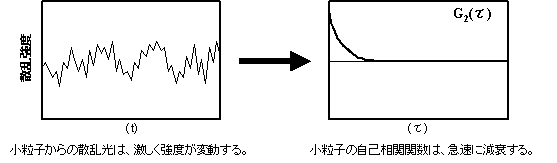
図１２．小さな粒子からの散乱光の揺らぎと自己相関関数


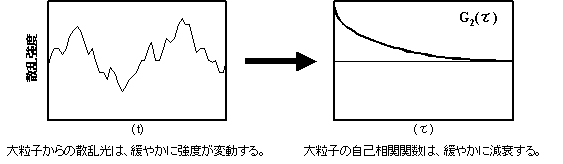
図１３．大きな粒子からの散乱光の揺らぎと自己相関関数