分子量測定
2.光散乱理論 … 気体中、溶液中の散乱理論式、大きい分子からの散乱理論式
今回は、静的光散乱法(SLS法)による分子量測定の原理をご紹介します。
粒子および分子に電磁波(光)が当たると、粒子及び分子の電子がエネルギーを吸収し、振動を始めます。振動している電子からは電磁波(光)があらゆる方向に放出され散乱現象となります。
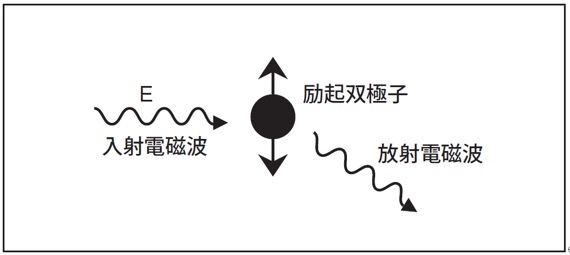
この放射電磁波(散乱光)の強度を、濃度や角度を変えながら測定し解析することで、溶液中の分子の分子量を測定します。
なお、この章は数式が多く出てきますので、「数式は苦手だな…」という方は、3.SLSの測定方法にお進み下さい!
● 気体中の粒子の散乱
ここではまず、気体中の粒子による光散乱を考えます。
散乱強度(Is)と入射光の強度(Io)の比は、入射光は垂直偏向のレーザーを使用する場合には、次式で与えられます。
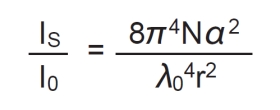
N:分子の数
λo:入射光の波長
r:物質から検出器までの距離
α:分子の分極率
この、散乱強度が入射光の波長λの4乗に反比例する式を、Rayleighのλ-4則と呼びます。
なお、分極率αは次式で表されます。
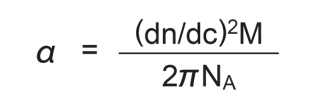
dn/dc:屈折率の濃度増分
M:分子量
NA:アボガドロ数
これらの式より、散乱光の強度から分子量を求めることが出来ます。
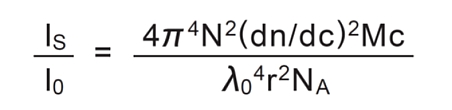
● 溶液中の散乱
溶液中では分子と溶媒の熱力学的相互作用を考慮する必要があり、式は次のようになります。
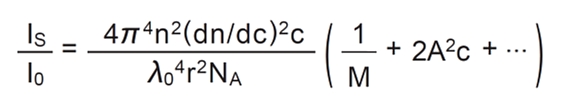
また、 R(θ)=Is r2 Io をレーリー比と呼び、光学定数 K=(4π2n2/λo 4NA)(dn/dc)2と置くことにより、次式のように表すことが一般的です。
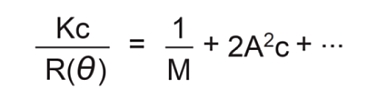
● 大きい粒子(分子)の散乱
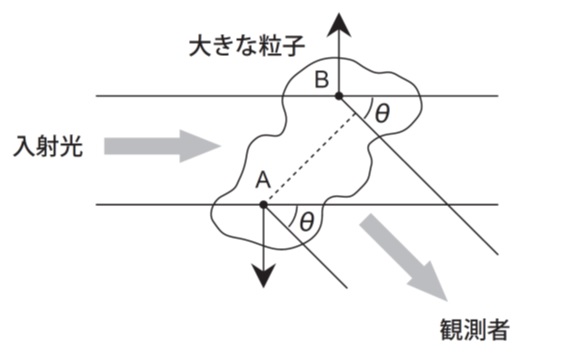
粒子が波長以上の大きさになると粒子のあらゆる部分から散乱が干渉し合って散乱強度に角度依存性が現れます。これをP(θ)関数として表すと、式は次のようになります。
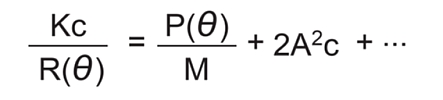
●重量平均分子量解析(Zimmプロットを例にして)
分子量が大きくなったり、溶液中で分子が広がっていると、同一分子上の複数の点からの散乱光が干渉を起こし、角度依存性が出てきます。ガウス鎖でかつ分布がある場合、慣性自乗半径のZ平均値<S2>から得られる慣性半径(radius of gyration)<S2>1/2および重量平均の絶対分子量Mwにより近似的に散乱強度を表し、散乱ベクトル q=(4πn/λo)sin(θ/2) を使って、実際に使いやすいプロットの形にしています。
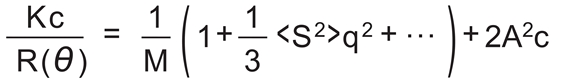
横軸にKc/R(θ)、横軸にsin(θ/2)+Bcでプロットしたのが、Zimmプロットです。(Bは任意の定数)この式に基づいて、Kc/R(θ)をsin2(θ/2)+Bcに対してプロットすると、c→0,θ→0への外挿より分子量Mを、各濃度のθ→0の点を結ぶ線の初期勾配より第二ビリアル係数A2を、各測定角度のc→0の点を結ぶ線の初期勾配より慣性半径<S2>1/2が求められます。標準ポリスチレン(TOSO製F-40)のベンゼン溶液の例を示します。
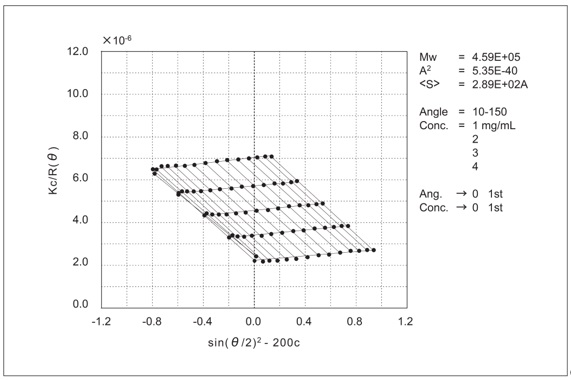
図2-1. 標準ポリスチレン(TOSO製F-40(TS-85);ベンゼン溶液)のZimmプロット
次回:
光散乱理論 … SLSの測定方法 … 光学系の概念図と、測定の流れ


 Close
Close

