偏光解消動的光散乱法によるカーボンナノチューブの軸比の測定
垂直方向に偏光した入射光をサンプルに照射した時、偏光子を垂直方向にして測定される散乱光は偏光散乱といい、IVVで示されます。一方、偏光子を水平方向にして測定される散乱光は偏光解消散乱といい、IHVで示されます。偏光散乱は、主に粒子の並進運動に依存するのに対して、偏光解消散乱は散乱媒体中の粒子の光学的な異方性に由来します。
もし、粒子が球形ならば、偏光解消散乱はゼロに等しくなりますし、棒状粒子のように粒子が回転しているのであれば、その運動に対応して、偏光解消成分の強度が変動することになります。つまり、光学的に異方性の粒子の回転についての情報を含んでいることになります。
今、検出器の前の偏光子を水平方向にして、動的光散乱測定をおこなうと、上述した理由により、粒子の回転に関する情報(回転拡散係数)を得ることができます。
このときの相関関数は式(1)に表されます。
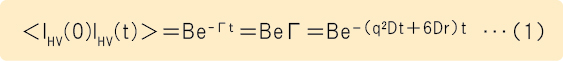
ここで、Dtは並進拡散係数、Drは回転拡散係数、q(=4πnsin(θ/2)/λ)は散乱ベクトル
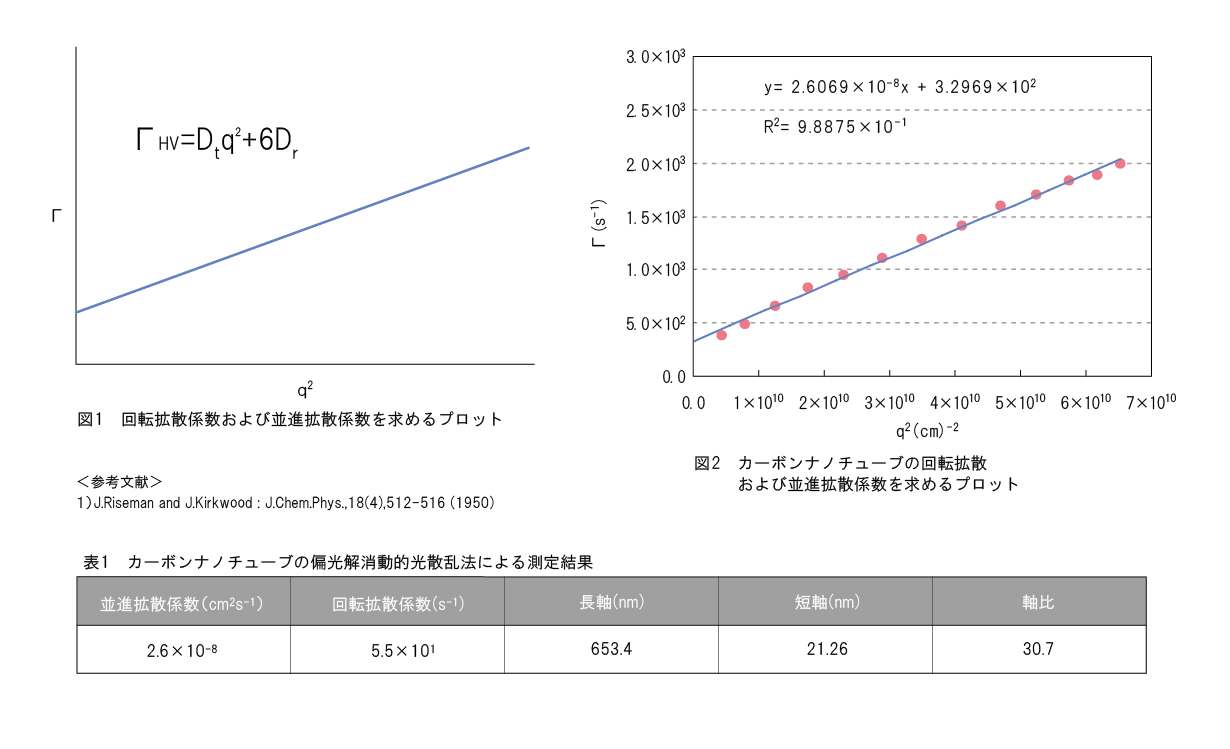
図1のように横軸q2に対し、縦軸にΓ(減衰定数)をプロットする(測定角度を変えて偏光解消散乱の動的光散乱測定をおこない、減衰定数を求めてプロットする)と、切片の1/6がDr、傾きがDtとして求められます。
DrとDtからは、(2)式のKirkwood-Riseman1)の関係式を用いて、長軸(L)と短軸の長さ(d)が算出されます。
すなわち、軸比(アスペクト比)はL/dによって求められます。
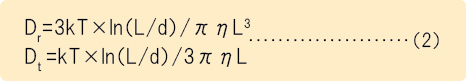
ここで、T:絶対温度、k:ボルツマン定数、η:媒体の粘性率
偏光解消動的光散乱法では、並進運動の情報の他に、異方性粒子(ロッド状粒子)の回転についての情報(回転拡散係数)が得られます。求めた回転拡散係数と並進拡散係数を用いて、Kirkwood-Risemanの関係式より、長軸(L)と短軸(d)の長さを求めることができ、軸比(アスペクト比)が算出されます。
今回、多層カーボンナノチューブ(Aldrich社製:長さ0.5~2.0μm、外径20~30nm、内径1~2nm)を濃度0.002wt%になるように、1%ドデシル硫酸ナトリウム水溶液に分散させ、偏光解消動的光散乱測定をおこないました。推定値内の結果が得られており、求めた軸比も妥当な結果であると推測されます。サンプルの分散条件をよくすることが必須ですが、偏光解消動的光散乱法はロッド状粒子の軸比を求めることが可能であり、貴重な情報を与えてくることが期待されます


 Close
Close

